array

What is an Array?

• Stores a collection of values in a contiguous block of memory
• Elements are located one after another with no space in between

How Data is Stored in Memory

• RAM (Random Access Memory)
  • All variables and data structures are stored
  • Composed of billions of bytes
• Byte
  • A byte is a unit of memory made up of 8 bits
• Bit
  • A bit is the most basic unit, representing a single binary digit, either a 0 or a 1

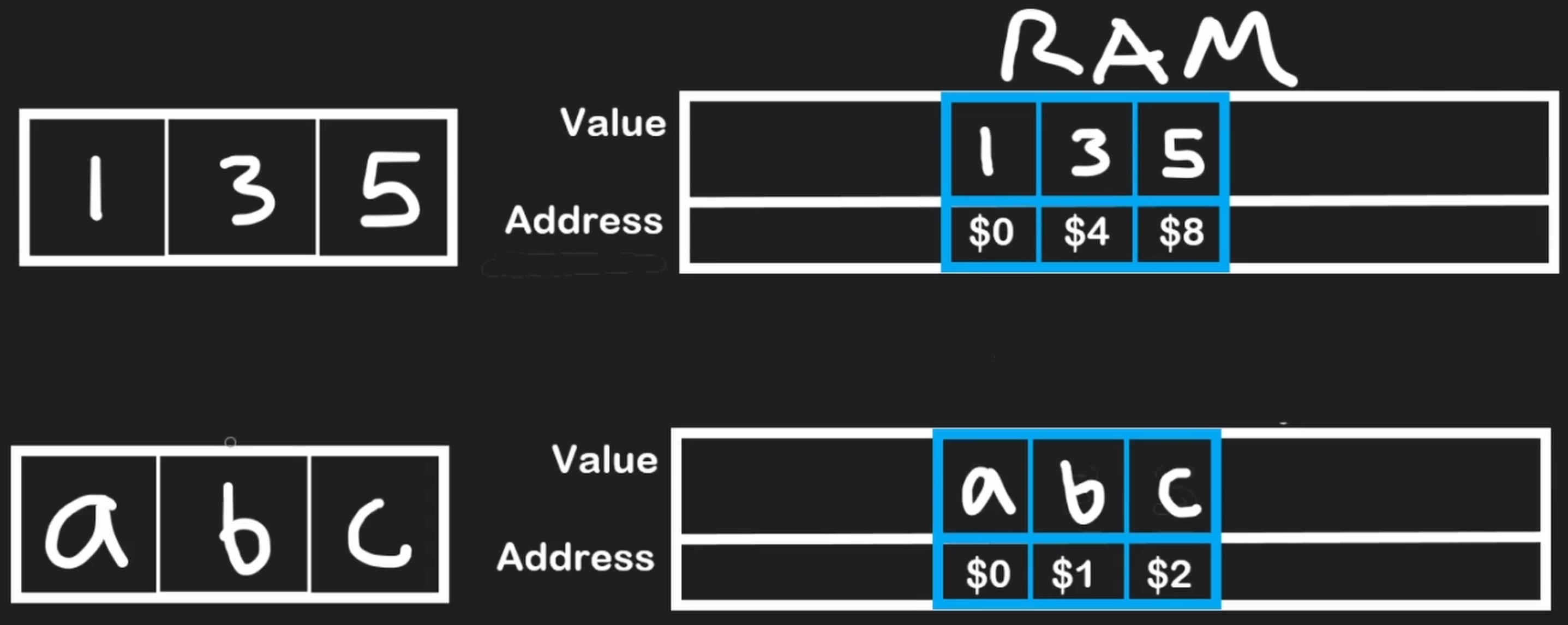
Each element's location in memory has a unique address. Because they are stored sequentially, the address for each subsequent element increases by a fixed amount determined by the data type's size

• Integer: An integer commonly requires 4 bytes of storage (e.g., address 0, address 4, address 8)
• Character: A single character typically only needs 1 byte (e.g., address 0, address 1, address 2)

Static vs. Dynamic Arrays

• Static: Have a fixed size determined at creation. You can't add or remove elements
  • Examples: C++ (int[]), Java (double[])
• Dynamic: Are resizable. You can add or remove elements as needed
  • Examples: C++ (std::vector), Java (ArrayList), Python (list)

How Dynamic Arrays Work

Dynamic arrays manage a block of memory with a certain capacity

• If you don't specify the size, it will initalize it to some default size depending the programming langauge
• There is a pointer to save the last element of the array
• Size: The number of elements currently in the array
• Capacity: The total number of elements the array can hold before needing to resize

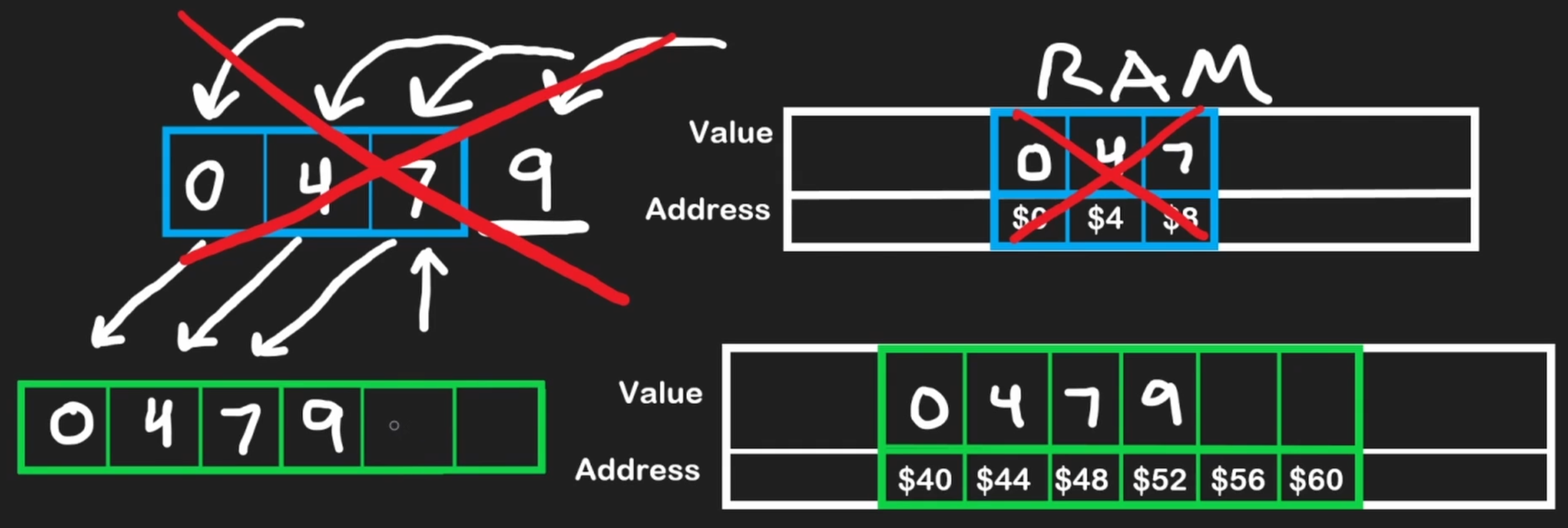
When the size exceeds the capacity, the array automatically

• Allocates a new, larger block of memory (often double the size)
• Copies all existing elements to the new location → O(n) operation
• Add the new element
• Deallocates the old memory block

Amortized Complexity

Amortized complexity is the average cost of an operation over many operations. Rare, expensive operations are offset by frequent, cheap ones, spreading high costs for a realistic performance measure

How it applies to a dynamic array

• The action: Adding an element to the end of the array
• The cheap case O(1): When there’s empty space, adding an element is instant
• The expensive case O(n): When full, a resize is needed
  • Create a new, larger array (usually double the size)
  • Copy all elements from the old array (O(n) time, where n is the current number of elements)
• The amortized result O(1): Resizes are infrequent. After one resize, many O(1) additions occur before the next resize. Averaging total cost over all additions yields a constant cost per addition, so the amortized time complexity is O(1)

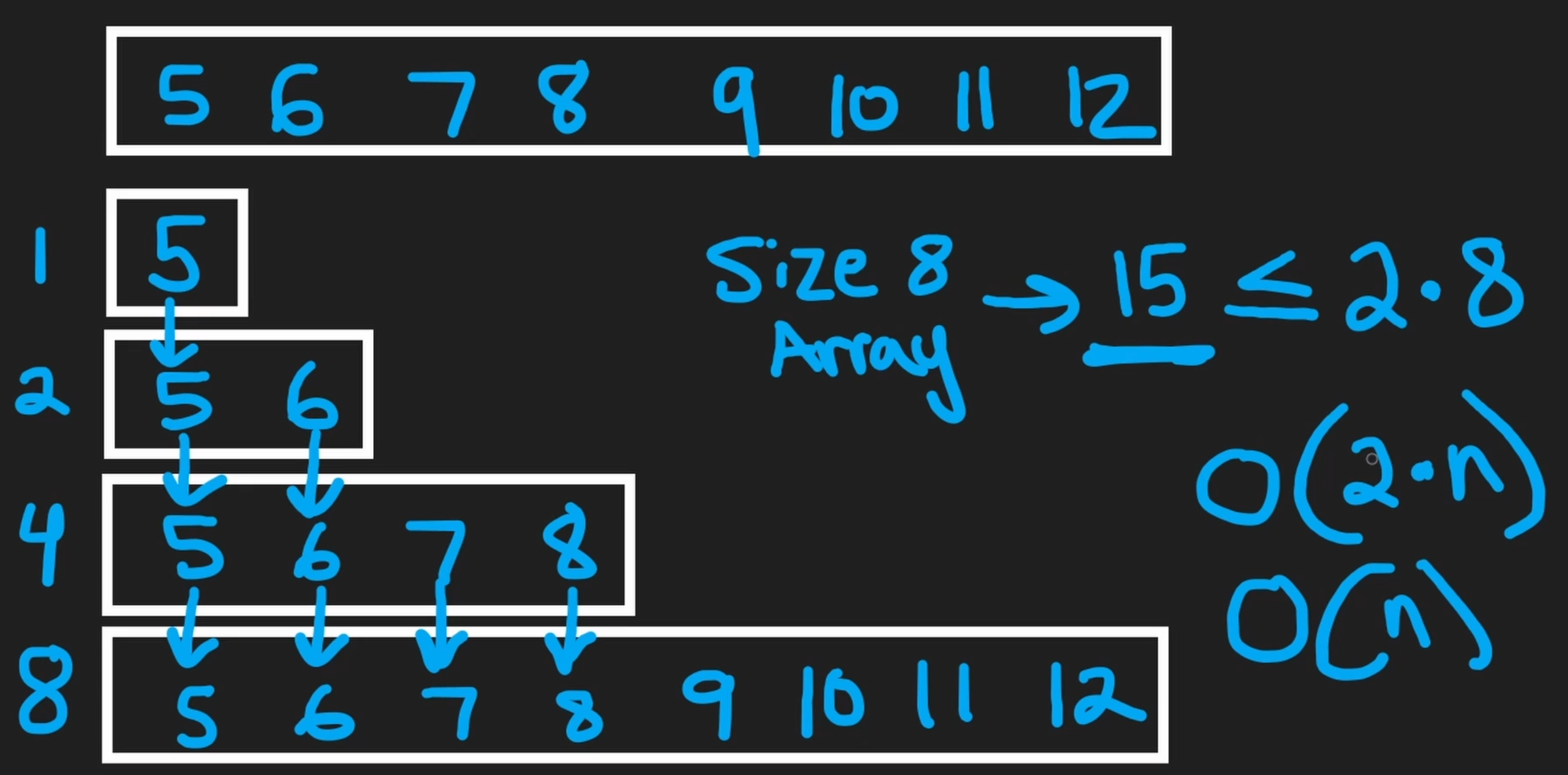
Example (size 8 array)

• For 8 elements
  • 8 insertions
  • 7 copy operations during resizes (1 for size 1 → 2, 2 for 2 → 4, 4 for 4 → 8)
  • Total cost: 8 (insertions) + 7 (copies) = 15 operations
  • 15 <= 2 * 8 (16), so total cost for n elements is ~ O(2n)

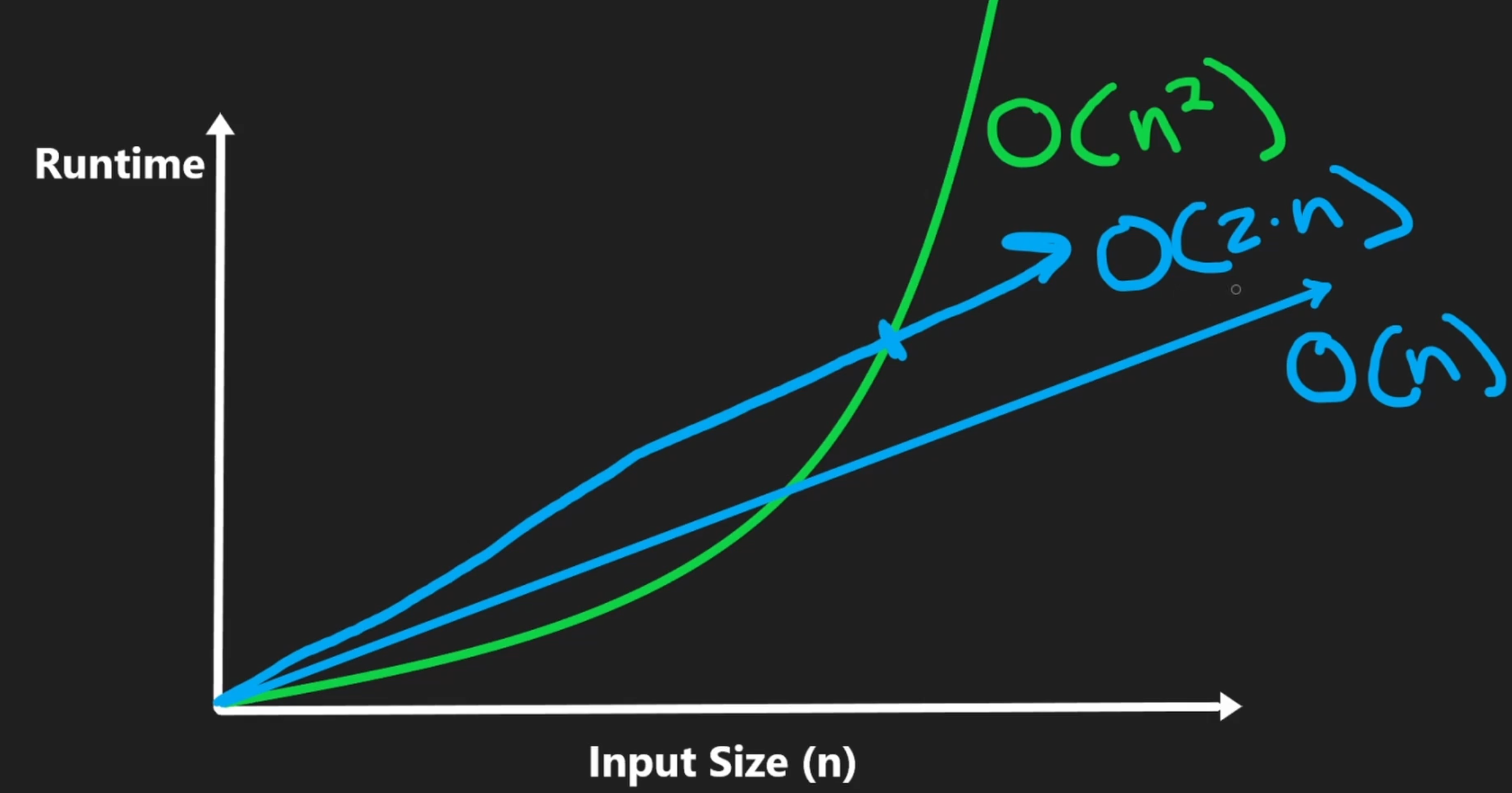
O(2n) vs. O(n)

• In Big O, constants (e.g., 2) are ignored, so O(2n) simplifies to O(n)
• Average cost per insertion: O(2n)/n = O(2) → O(1) after ignoring constants
• This is amortized time complexity: rare, costly resizes are spread over many fast O(1) insertions

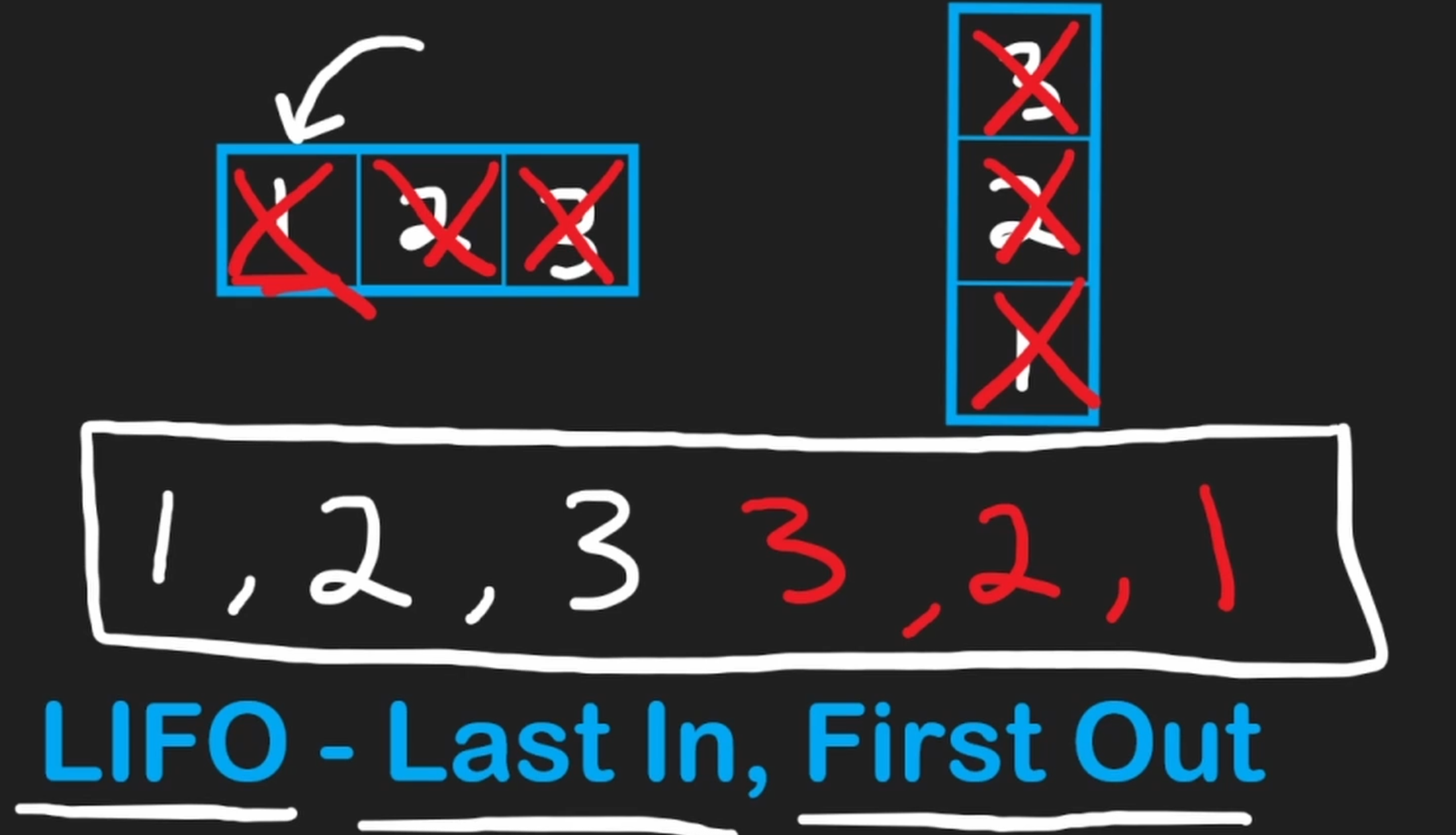
Stack

A stack is a common data structure that supports three main O(1) (constant time) operations

• Push: Adds an element to the end (top) of the stack
• Pop: Removes an element from the end of the stack
• Peek: Looks at the last element without removing it

The defining principle of a stack is LIFO (Last-In, First-Out), which means the last element added is the first one to be removed. A primary use case for this behavior is reversing a sequence of elements, like a string

Complexity

Static arrays

• Read/Access: O(1)
• Update: O(1)
• Append/Remove from the end: O(1)
• Insert/Remove from the middle: O(n)
  • It requires shifting subsequent elements

Dynamic arrays

• Read/Access: O(1)
• Append/Remove from the end: O(1) amortized
• Insert/Remove from the middle: O(n)

Stack

• Push/Pop/Peek/Top: O(1)