recursion

What Is Recursion?

Recursion is solving a problem by breaking it down to smaller instances of the same problem
- Factorial function: n! = n * (n-1)!
- Fibonacci sequence: f(n) = f(n-1) + f(n-2)
- In nature, they are like a tree
In programming, recursion is a concept where a function calls itself
Applications: Sorting algorithms (merge sort, quick sort), graph algorithms (DFS), etc.

Implementation

Base case: Stopping condition, allows recursion to terminate
Recursive case: breaks problem into smaller ones

Factorial

Code

def factorial(n: int) -> int:
  # base case
  if n == 0:
      return 1
  # recursion
  return n * factorial(n - 1)

How it works with factorial(3)

Call
3 * factorial(2) => It pauses the current work and goes to calculate factorial(2)
  2 * factorial(1) => It pauses the current work and goes to calculate factorial(1)
    1 * factorial(0) => It pauses the current work and goes to calculate factorial(0)
      factorial(0) returns 1 (Base Case)

Return
    factorial(1) = 1 * 1 = 1
  factorial(2) = 2 * 1 = 2
factorial(3) = 3 * 2 = 6

Complexity

Finding a tight bound of recursive algorithm is hard
Can be estimated based on number of calls to the method
Number of calls: O(n)
Each call: O(1) time, O(1) memory
Total: O(n) time, O(n) memory

How to calculate time complexity

For factorial(n), the tree structure looks like this
- Nodes: Each function call is a node. The initial call is the root
- Edges: Each recursive call creates a child node, so an edge represents the invocation from a caller to a callee
- Work per node: We need to determine the amount of work done at each node, excluding the recursive calls themselves
Calculating time complexity
- Work at each node: In each call to factorial(n), we perform two main operations
  - One comparison (n == 0)
  - One multiplication (n * ...)
  - These operations take a constant amount of time. Let's denote this constant work as c
- Depth of the tree: The recursion continues until n becomes 0. The initial call is factorial(n), then factorial(n-1), and so on, down to factorial(0). This creates a total of n + 1 levels or a depth of n
- Total work: To find the total time complexity, we sum the work done at each node in the tree
  - factorial(n) does c work
  - factorial(n-1) does c work
  - ...
  - factorial(1) does c work
  - factorial(0) does c work (just the comparison)
- Since there are n + 1 nodes in our "tree" (which is essentially a single branch), the total work is the sum of the work at each level
  - Total work = Σ_{i=0}^{n} c = c * (n + 1)
  - O(c * (n + 1)) = O(n)

How to calculate the space complexity

For a recursive function, the primary space cost comes from the call stack. Each time the function calls itself, a new stack frame is pushed onto the stack. This frame stores the function's state, like the value of its local variables (in this case, n) and the return address. The space complexity is determined by the maximum number of frames on the stack at any single point in time
Let's trace the call stack for factorial(4)
- factorial(4) is called. The stack has one frame
  - [ factorial(4) ]
- factorial(4) calls factorial(3). The stack grows
  - [ factorial(4), factorial(3) ]
- This continues until the base case is reached. The stack is at its deepest when factorial(0) is called
  - [ factorial(4), factorial(3), factorial(2), factorial(1), factorial(0) ]
At its peak, the call stack holds n + 1 frames (from n down to 0). Once factorial(0) returns, the stack unwinds, and frames are popped off
Since the maximum memory required is proportional to the number of stack frames, and that number is n + 1, we simplify this to O(n) in Big O notation. This means the space required grows linearly with the input value n

Fibonacci

Code

def fibonacci(n: int) -> int:
  # base case
  if n < 2:
      return n
  # recursion
  return fibonacci(n - 1) + fibonacci(n - 2)

How it works with fibonacci(4) (in order)

Call
fibonacci(4) = fibonacci(3) + fibonacci(2)
  fibonacci(3) = fibonacci(2) + fibonacci(1)
    fibonacci(2) = fibonacci(1) + fibonacci(0)
      fibonacci(1) returns 1 (Base Case)
      fibonacci(0) returns 0 (Base Case)
    fibonacci(1) returns 1 (Base Case)
  fibonacci(2) = fibonacci(1) + fibonacci(0)
    fibonacci(1) returns 1 (Base Case)
    fibonacci(0) returns 0 (Base Case)

Return
    fibonacci(2) = 1 + 0 = 1
  fibonacci(3) = 1 + 1 = 2
  fibonacci(2) = 1 + 0 = 1
fibonacci(4) = 2 + 1 = 3

First, fibonacci(3) = fibonacci(4) -> fibonacci(3) -> fibonacci(2) -> fibonacci(1) and fibonacci(0)
Then, fibonacci(2) = fibonacci(2) -> fibonacci(1) and fibonacci(0)

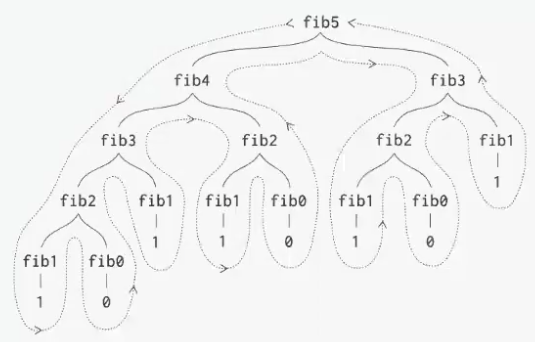
How to calculate time complexity

Work at each Node: Just like with factorial, each fibonacci call does a constant amount of work (one comparison and one addition). Let's consider the cost of each node to be 1
Total work: The total time complexity is the total number of nodes in the tree. To find this, we can analyze the tree's structure
- Depth: The tree has a depth of n. The longest path follows the fib(n-1) calls (e.g., fib(4) -> fib(3) -> fib(2) -> fib(1))
- Nodes per Level: At each level k, there are roughly 2^k nodes. This isn't perfectly accurate because the tree is "lopsided" (the right side is always shorter than the left), but it provides a good upper bound
Summing the work: The total number of nodes is approximately the sum of nodes at each level, which is roughly: 2^0 + 2^1 + 2^2 + ... + 2^{n-1}
- This is a geometric series that sums to 2^n - 1
In Big O notation, we drop the constant -1, so the time complexity is: O(2^n)

How to calculate space complexity

While the time complexity is exponential (O(2^n)) due to the total number of calls, the space complexity is determined by the maximum depth of the call stack at any single moment, not the total number of nodes in the recursion tree
Let's trace the execution for fibonacci(4) to see how the call stack behaves. The execution will proceed down the "leftmost" branch of the tree first
- fibonacci(4) is called
  - Stack: [ fib(4) ]
- It calls fibonacci(3)
  - Stack: [ fib(4), fib(3) ]
- fibonacci(3) calls fibonacci(2)
  - Stack: [ fib(4), fib(3), fib(2) ]
- fibonacci(2) calls fibonacci(1)
  - Stack: [ fib(4), fib(3), fib(2), fib(1) ]
- This is the deepest point the call stack will reach for the n=4 example. The stack has a depth of n
- fibonacci(1) returns. Its frame is popped off the stack
  - Stack: [ fib(4), fib(3), fib(2) ]
- Now, fibonacci(2) calls fibonacci(0). The stack grows again but does not exceed its previous maximum depth
  - Stack: [ fib(4), fib(3), fib(2), fib(0) ]
The key insight is that the fibonacci(n-2) branch is only explored after the fibonacci(n-1) call has returned and its stack frames have been popped. Therefore, the maximum number of frames on the stack at any one time is determined by the depth of the longest path in the recursion tree, which is n
Because the maximum depth of the call stack is directly proportional to the input n, the space complexity is O(n)

Recursive vs. Iterative

Recursive	Iterative
Function calls itself, until base case is reached	Loop until end condition is met
Tends to be more memory-intensive due to the call stack	More memory-efficient
More overhead due to function calls	No overhead from function calls
(Usually) More concise, elegant, mathy code	Easier to debug
Suitable for problems that can be naturally broken down into subproblems (sorting) or trying all possibilities (backtracking)	Suitable for problems requiring sequential operations

Base Knowledge

Factorial Function

Meaning

The factorial of a natural number n (denoted as n!) is the product of all positive integers from 1 up to n
- Example: 5! = 5 * 4 * 3 * 2 * 1 = 120

Explaining the formula n! = n * (n-1)!

This formula describes the factorial recursively. Let's break it down with the 5! example
- According to the formula, 5! = 5 * (5-1)! = 5 * 4!
- Similarly, to calculate 4!, we apply the formula again: 4! = 4 * (4-1)! = 4 * 3!
- This continues as follows: 3! = 3 * 2! and 2! = 2 * 1! and 1! = 1 * 0!
This process stops at a point called the "base case". For factorials, the base case is defined as: 0! = 1

As you can see, the formula n! = n * (n-1)! is a concise and elegant way to define the calculation of any factorial by reducing it to the problem of calculating the factorial of a smaller number

Fibonacci Sequence

Meaning

The Fibonacci sequence is an infinite series of numbers where each number (from the third one onwards) is the sum of the two preceding ones
The sequence most commonly starts with 0 and 1 (or sometimes 1 and 1). By the most common convention, the sequence is: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
- 1 = 0 + 1 and 2 = 1 + 1 and 3 = 1 + 2 and 5 = 2 + 3, and so on

Explaining the formula f(n) = f(n-1) + f(n-2)

This formula defines the n-th Fibonacci number (denoted as f(n)) based on the two numbers that come directly before it, f(n-1) and f(n-2)
For this formula to work, it also needs "base cases". These are the first two numbers in the sequence: f(0) = 0 and f(1) = 1
Now, let's use the formula to find a few numbers in the sequence
- f(2): f(2) = f(1) + f(0) = 1 + 0 = 1
- f(3): f(3) = f(2) + f(1) = 1 + 1 = 2
- f(4): f(4) = f(3) + f(2) = 2 + 1 = 3
- f(5): f(5) = f(4) + f(3) = 3 + 2 = 5

The Fibonacci sequence appears frequently in nature, such as in the arrangement of flower petals, the branching of trees, or the spiral patterns of seashells

What Is Recursion?​

Factorial​

Fibonacci​

Recursive vs. Iterative​

Base Knowledge​

Factorial Function​

Fibonacci Sequence​