big-o

Introduction to Big-O

Big-O notation is a mathematical framework for analyzing algorithm efficiency by describing how the number of operations grows with input size (n). It focuses on long-term behavior, ignoring constants and lower-order terms to classify algorithms into growth rate "families."

Purpose

• Compare algorithms: Enables objective efficiency comparisons for large datasets
• Analyze scalability: Predicts performance as input size increases, critical for scalable systems
• Abstract details: Focuses on the algorithm's core structure, independent of hardware or language specifics

Core Concepts

Growth Rate (Asymptotic Behavior)

Big-O examines how an algorithm performs as n approaches infinity, using asymptotic analysis

• Marathon analogy: O(n) (linear) is like a marathon runner with steady pacing, scaling better for large n. O(n^2) (quadratic) is like a sprinter, fast for small n but slowing dramatically as n grows
• Example: Linear (f(n) = 2n) grows steadily (each n adds 2), while quadratic (g(n) = n^2) accelerates explosively (larger n causes bigger jumps)

Dominant Term

Big-O simplifies complex functions (e.g., T(n) = 5n^2 + 1000n + 5000) to the fastest-growing term (O(n^2))

• Car engine analogy: The dominant term (n^2) is like a car's engine (e.g., V8), defining performance, while constants (5) and lower-order terms (1000n, 5000) are like a stereo or paint job—minor in the long run

Upper Bound

Big-O provides a worst-case performance guarantee

• Elevator analogy: Like a "Max Load: 500 kg" sign, O(n) guarantees an algorithm's operations won't exceed a linear function for large n, though best-case performance (e.g., O(1)) may be better
• Definition: A function f(n) is O(g(n)) if there exist positive constants c and n₀ such that f(n) ≤ c × g(n) for all n ≥ n₀

Proving Big-O

Lock and Key Analogy

• Lock: The Big-O definition tests if a function's growth stays at or below g(n)
• Key: A pair (c, n₀) satisfying the inequality
• Proof: Finding one valid (c, n₀) confirms f(n) is O(g(n))

Example: Proving T(n) = n^2 + 1000n + 6000 is O(n^2)

• Goal: Find c, n₀ such that n^2 + 1000n + 6000 ≤ c × n^2 for all n ≥ n₀
• Steps
  • For n ≥ 1: 1000n ≤ 1000n^2 (since n ≤ n^2), and 6000 ≤ 6000n^2 (since 1 ≤ n^2)
  • Substitute: n^2 + 1000n + 6000 ≤ n^2 + 1000n^2 + 6000n^2 = 7001n^2
  • Choose c = 7001, n₀ = 1
• Result: T(n) ≤ 7001n^2 for n ≥ 1, proving T(n) is O(n^2)

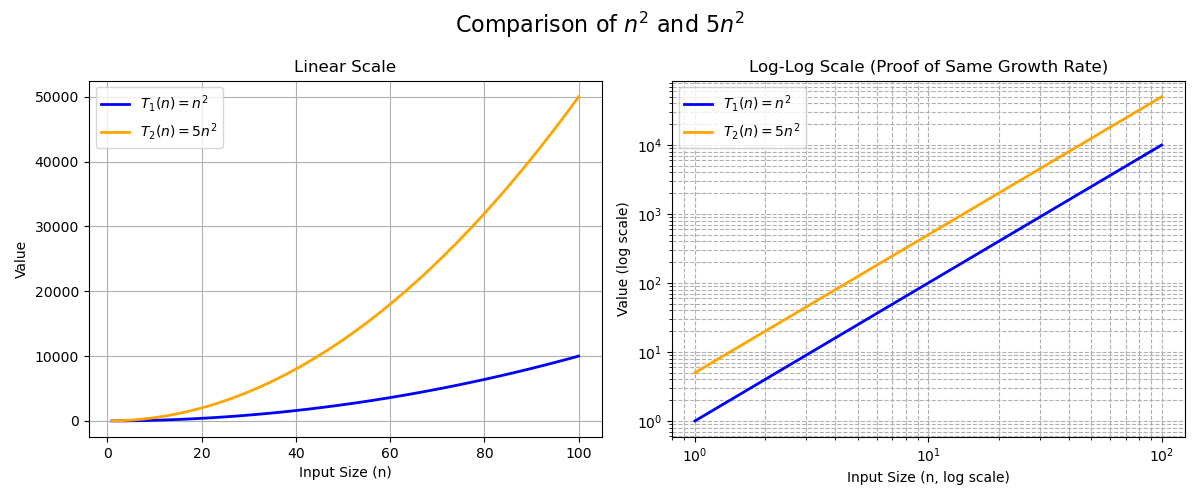
Why Constants Are Ignored

Constants (e.g., 5 in 5n^2) are scaling factors that don't affect growth rates

• Zoologist analogy: A Corgi (n^2) and Husky (5n^2) differ in size but belong to the same "Dog" species (O(n^2))
• Reasoning
  • Constants scale values but not growth (e.g., 5n^2 and n^2 both quadruple when n doubles)
  • Big-O focuses on n approaching infinity, where constants are negligible compared to higher-degree terms (e.g., n^3 outpaces 1000n^2)
  • Ensures hardware- and implementation-independent comparisons

Comparing Growth Rates

To compare growth rates of f(n) and g(n)

• Compute ratio: f(n)/g(n)
• Evaluate: limit as n approaches infinity of f(n)/g(n)
• Interpret
  • Finite positive constant (e.g., 5): Same growth rate
  • 0: f(n) grows slower
  • Infinity: f(n) grows faster

Example: f(n) = 5n^2 + 3n, g(n) = n^2

• Ratio: (5n^2 + 3n)/n^2 = 5 + 3/n
• Limit: limit as n approaches infinity of (5 + 3/n) = 5
• Conclusion: Same growth rate (O(n^2))

Example: f(n) = 10n^2 + 100n + 1000, g(n) = n^2

• Ratio: (10n^2 + 100n + 1000)/n^2 = 10 + 100/n + 1000/n^2
• Limit: limit as n approaches infinity of (10 + 100/n + 1000/n^2) = 10
• Conclusion: Same growth rate (O(n^2))
• Values

n	f(n)	g(n)	Difference (f(n) - g(n))	Ratio (f(n)/g(n))
10	3,000	100	2,900	30
100	111,000	10,000	101,000	11.1
1,000	10,101,000	1,000,000	9,101,000	10.101

• Ratio approaches 10, confirming same growth rate

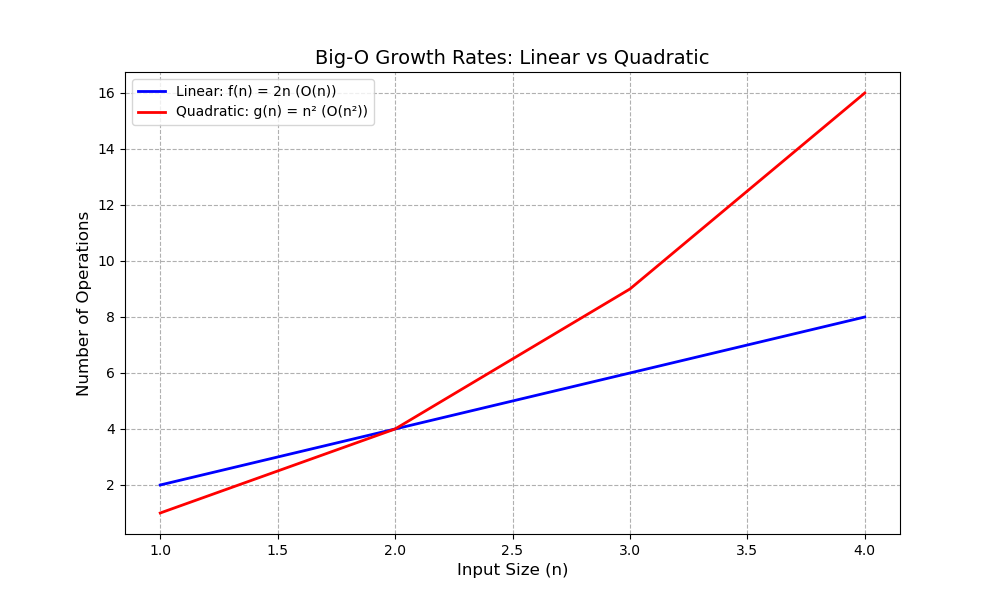
Linear vs. Quadratic Growth Examples

Linear Growth

Function: f(n) = 2n

• When n increases from 1 to 2, f(n) goes from 2 to 4 (increase by 2)
• When n increases from 10 to 11, f(n) goes from 20 to 22 (increase by 2)
• Conclusion: Growth is steady; each n increase by 1 adds a constant amount (O(n))

Quadratic Growth

Function: g(n) = n^2

• When n increases from 1 to 2, g(n) goes from 1 to 4 (increase by 3)
• When n increases from 10 to 11, g(n) goes from 100 to 121 (increase by 21)
• Conclusion: Growth accelerates rapidly; larger n causes bigger jumps (O(n^2))

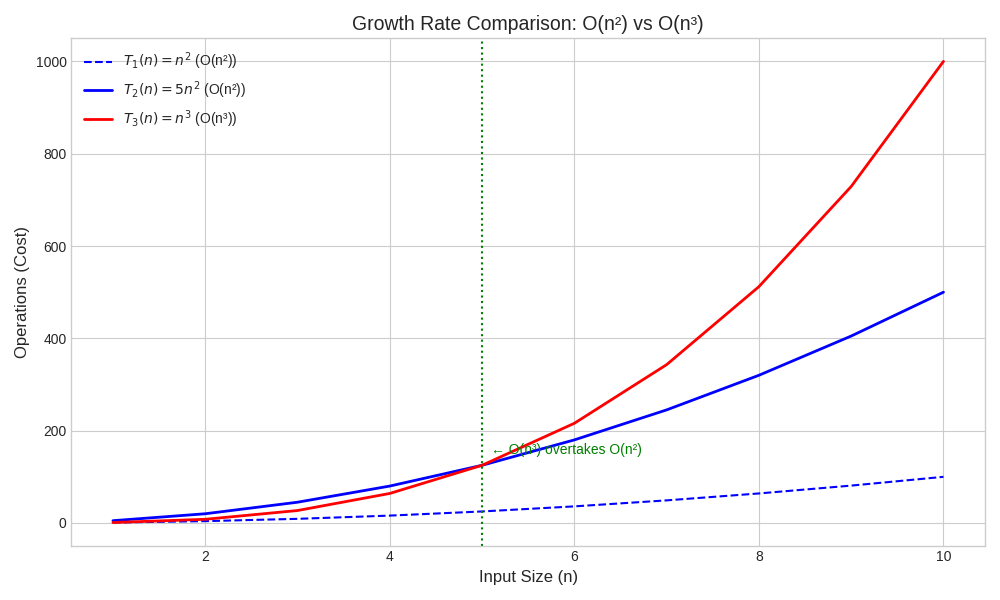
Practical Insights From T(n) = O(n^2)

• Scalability: Runtime grows approximately 100x if n grows 10x (10^2)
• Bottleneck: Nested loops likely cause the n^2 complexity
• Ranking: Less efficient than O(n log n) but better than O(n^3)

Common Big-O Classes

• Logarithmic Time: O(log n)
  • Example: Binary Search
  • Meaning: Highly efficient, ~30 steps for 1 billion items
• Linear Time: O(n)
  • Example: T(n) = 500n + 20000
  • Meaning: Cost grows proportionally (e.g., array scanning)
• Linearithmic Time: O(n log n)
  • Example: T(n) = 2n log n + 30n + 100
  • Meaning: Efficient for sorting (e.g., Merge Sort)
• Quadratic Time: O(n^2)
  • Example: Bubble Sort
  • Meaning: Common in algorithms with nested loops, less scalable
• Exponential Time: O(2^n)
  • Example: T(n) = n^4 + 3n^2 + 2^n
  • Meaning: Brute-force algorithms, unscalable for n > 50

Bubble Sort Analysis

Basic Bubble Sort

• Worst Case (e.g., [n, n-1, ..., 1])
  • Outer loop: n iterations
  • Inner loop: n(n-1)/2 ≈ n^2/2 comparisons
  • Swaps: Up to n(n-1)/2
  • Total: ~n^2 operations
  • Big-O: T₁(n) ≈ n^2 → O(n^2)

Optimized Bubble Sort

• Worst Case
  • Comparisons: n(n-1)/2 ≈ n^2/2
  • Swaps: Up to n(n-1)/2
  • Swapped flag checks: ~n (negligible)
  • Total: ~n^2 operations
  • Big-O: T₂(n) ≈ n^2 → O(n^2)
• Best Case (e.g., [1, 2, ..., n])
  • One iteration, n-1 comparisons, 0 swaps
  • Big-O: O(n)

Comparison

• Worst Case: Both are O(n^2), with ~n(n-1)/2 comparisons
• Ratio: T₁(n)/T₂(n) ≈ 1 for comparisons, slightly higher (e.g., 1.1–1.2) with swaps and checks
• Example (n=5, [5, 4, 3, 2, 1])
  • Basic: 10 comparisons
  • Optimized: 10 comparisons + ~5 checks
  • Ratio: ~1
• Large n (n=1000)
  • Comparisons: ~499,500 for both
  • Optimized adds ~1000 checks (negligible)
  • Ratio: limit as n approaches infinity of T₁(n)/T₂(n) ≈ 1

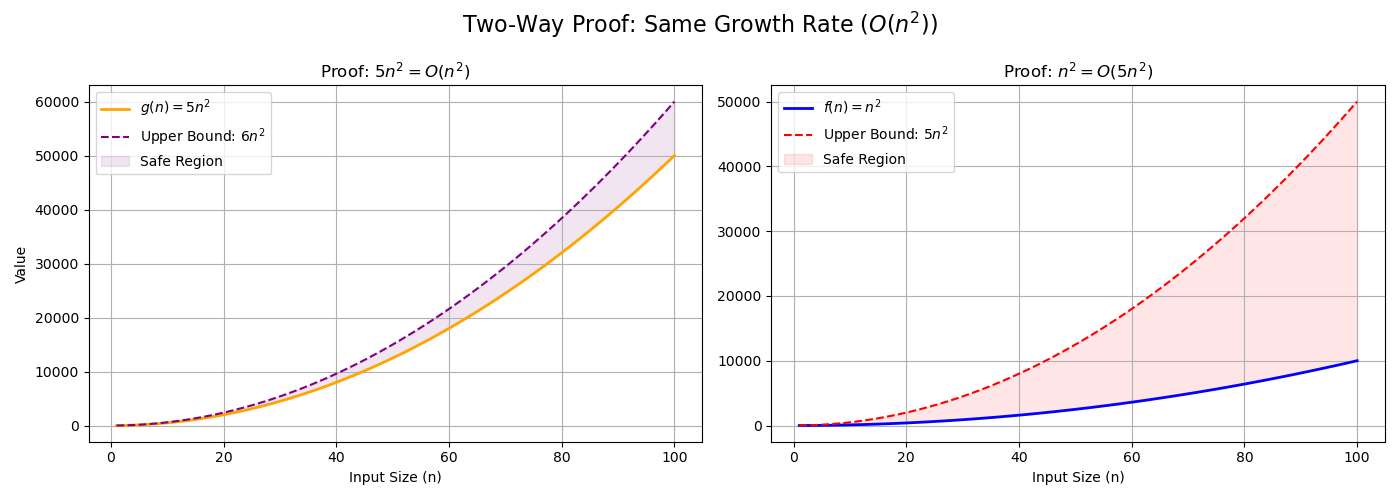
Understanding the Worst-Case and Upper Bound Gap

The gap between the worst-case function (e.g., f(n) = n) and the upper bound (e.g., c × n) represents a "safety margin."

• Worst Case (e.g., n): The actual cost in the worst scenario
• Upper Bound (e.g., 1.2 × n): The mathematical "ceiling" guaranteeing performance
• Example: Like promising to arrive before 5 PM but arriving at 4:50 PM—the 10-minute buffer is the gap

Why the Gap Exists

The gap arises from flexibility in choosing c in f(n) ≤ c × g(n)

• Example: For f(n) = n, g(n) = n
  • c = 1: n ≤ n (no gap)
  • c = 1.2: n ≤ 1.2n (visible gap)
  • c = 2 or 100: n ≤ 2n or n ≤ 100n (larger gap)
• Conclusion: Big-O requires only a valid c, not the tightest, allowing a buffer for simpler proofs

Why C × G(n) Is the Upper Bound

c × g(n) is the specific upper bound function—the ceiling f(n) never crosses for n ≥ n₀. O(g(n)) is the complexity class, indicating f(n) has an upper bound of the form c × g(n)

Benefits of Upper Bounds

• Guarantee: Ensures performance won't exceed the bound, critical for stable systems
• Prediction: Helps estimate scaling (e.g., O(n^2) means a 10x input increase leads to ~100x runtime increase)

Why Ignore the Constant C?

Big-O ignores c to focus on growth type, not exact speed

• Analogy: Algorithms costing 5n^2 and 7001n^2 are like two V8 engines—one tuned (c=5), one less so (c=7001). Both are O(n^2)
• Reasoning: c depends on external factors (e.g., programming language, hardware, compiler optimizations). Ignoring c ensures universal comparisons

Visualization

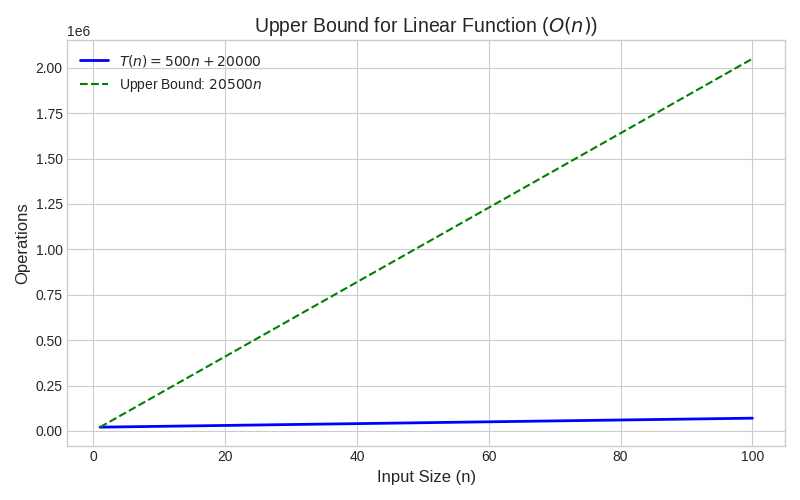
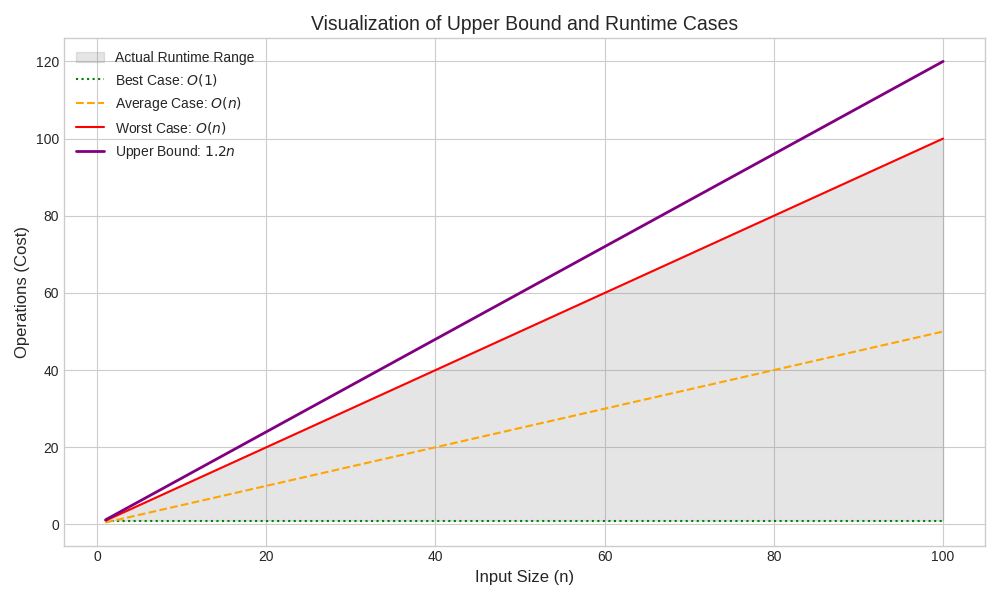
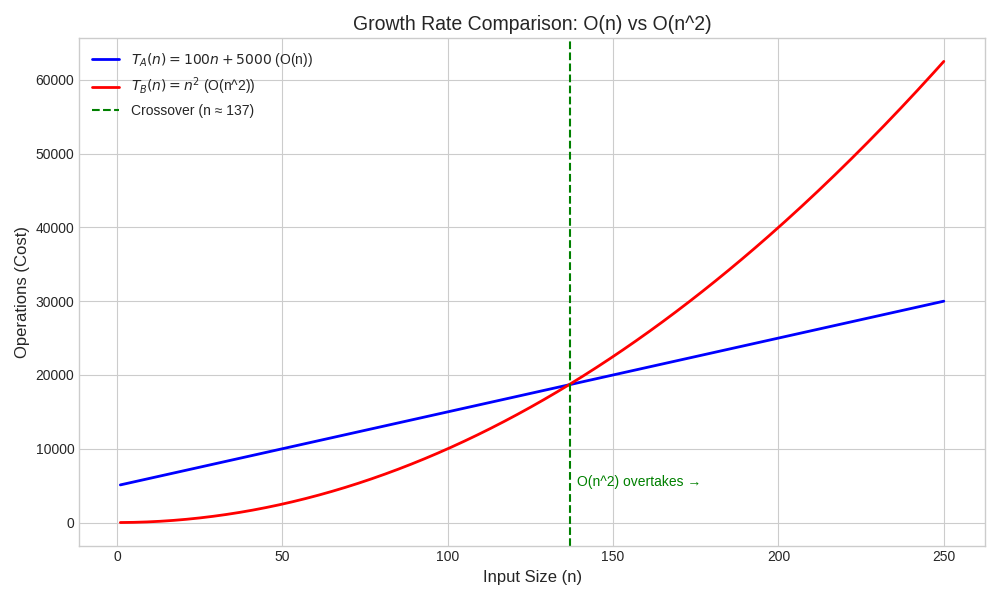
Conclusion

Big-O notation classifies algorithms by their dominant growth rate, ignoring constants (e.g., 5 in 5n^2) to focus on scalability. Functions like 5n^2, n^2, and 10n^2 + 100n + 1000 are all O(n^2). Bubble Sort (basic and optimized) has O(n^2) Worst-case complexity, but the optimized version achieves O(n) in the best case. The gap between worst-case and upper bound reflects flexibility in choosing c, providing a safety margin for performance guarantees